We are pleased to announce that another one of the most asked for features is going to be a part of our SNP & Variation Suite™ software, Gene by Environment Interaction Regression (also known as GxE Regression). Earlier this year other highly asked for features were added to SVS including applying a prediction model to a new dataset, cross-validation for genomic prediction, and meta-analysis. It is safe to say that our customer requests have been instrumental in driving development this year!
Before this latest update, Numeric Regression was already a powerful workhorse, including full versus reduced model regression, moving window regression and step-wise regression. All of these regression models allowed for accounting for covariates of various types, for both logistic and linear regression (binary and quantitative dependent variables). Numeric Regression did allow for the option to add interaction terms, but these interactions had to be explicitly stated and were designed more for covariate by covariate interaction terms and not covariate by SNP or gene interactions.
In the past, we tried to solve this limitation with the aid of Python scripts (Linear and Logistic Regression with Interactions). This script worked for small numbers of genomic markers, but was too slow to be useful on the genome-wide scale. Now regressing covariates against each column or predictor is available using our core math libraries, implemented directly into the software. As a result, adding the interaction term into the model only takes 1 minute longer to compute the results for +384k SNPs compared to running the same analysis without the covariate-column interaction.
Let’s back up for a minute. What is a Gene x Environment Interaction Regression Model? Well, a typical regression model for a GWAS may be testing the null hypothesis that after correcting for various covariates (age, gender, BMI) the SNP does not contribute significantly to the model, and that in the case of an additive genetic model, more copies of the minor allele does not result in a significant change in the dependent variable.
A typical regression model with covariates and covariate by covariate interaction might be:
![]()
In the above model, if you exclude the BMI*gender interaction term, each covariate would be accounting for the effect that they have on blood pressure, then after correcting for the covariates, the model tests whether or not the SNP explains enough of the remaining variability of the blood pressure.
In Gene by Environment Interaction regression, the idea is that the effect of the environmental factor or covariate is different for different numbers of the minor allele (in the case of the additive model). The “environment” influences the genetic effect on the phenotype. Here is what a model might look like if we think that BMI might influence the genetic effect.
![]()
It was possible to test a single model like this in SVS, but if you wanted to test the GxE effect on all SNPs in a GWAS this was not so easy. Now it is as simple as selecting the covariate – column interaction option in the regression menu:
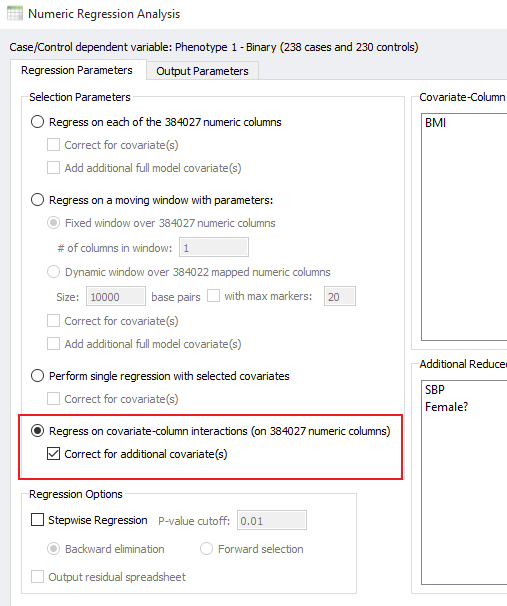
As with all regression models run through Numeric Regression, a summary of each model per SNP (or column) as well as detailed results are available. The summary spreadsheet includes these outputs:

| Column Name | Description |
| FvR Model P-Value | The p-value testing the hypothesis on whether the covariate-column interaction adds significantly to the model after correcting for the covariates (at a minimum the covariate and column used for the interaction term). |
| Full-Model P-Value | The p-value for the regression model that includes all covariates, the column, and the covariate-column interaction. |
| Mean Y | Mean of the dependent variable |
| Beta # | Coefficient of the specified term/covariate |
| Beta # SE | Standard error for the specified term/covariate |
| Beta pred | Coefficient of the column (predictor is identified by row label, and called predictor for the rest of the table) |
| Beta pred SE | Standard error for the predictor |
| Interaction # Beta | Coefficient of the interaction term between the covariate number indicated and the predictor. |
| Interaction # Beta SE | Standard error for the interaction term between the covariate number indicated and the predictor. |
| Reg. df Full Model | Regression degrees of freedom for the full model |
| Reg. df Reduced Model | Regression degrees of freedom for the reduced model |
| Residual df Full Model | Residual degrees of freedom for the full model |
| Chi-square Full Model (logistic) or F Full Model (linear) | Value of the test statistic for the full model |
| Chi-square Full vs. Reduced Model (logistic) or F Full vs Reduced Model (linear) | Value of the test statistic for the full versus reduced model |
| Sample Size | The sample size for the particular regression model |
The detailed results table includes the statistics for each covariate and interaction:
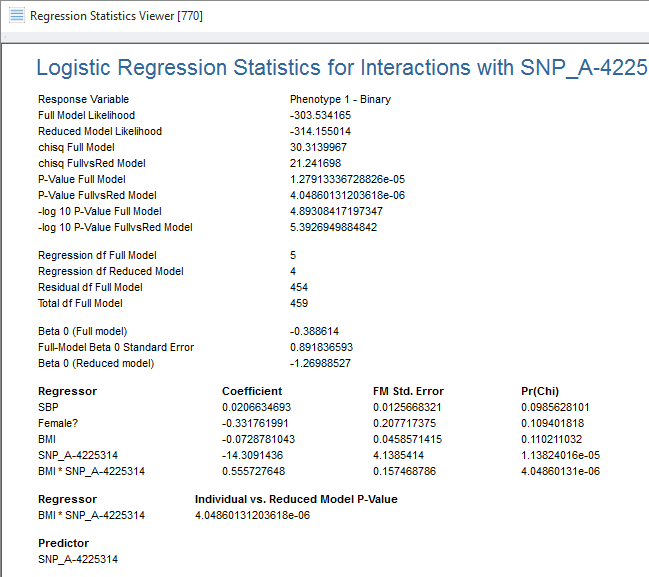
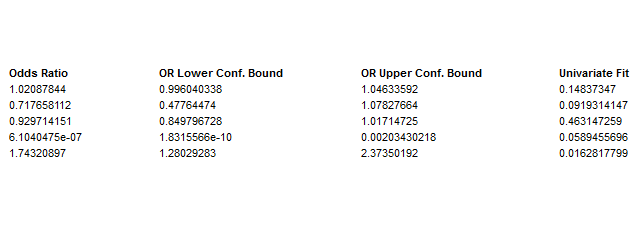 We anticipate having this available in our software in mid-September. If you would like to be notified when it is available, or have any suggestions for features you would like to see in SVS, please let us know!
We anticipate having this available in our software in mid-September. If you would like to be notified when it is available, or have any suggestions for features you would like to see in SVS, please let us know!